Raycasting ?

There's an awesome effect one can achieve once you have HDMA in a platformer: add depth to your background with "floors" like in DKC2 Lava lagoon. There will be complete occlusion of the 'far' background plane (wall) by the 'near' background plane (floor side), so having them scroll at different speed is 'just' a matter of updating X scrolling register at the right time. Having the floor positioned above or below the "seam line" between two walls is 'just' a matter of adjusting Y scrolling register earlier or later so that they 'skip' part of the far background art to show front background art.

The awesome part is that depth effect added with the horizontal planes, of course. That is about adjusting both X and Y scrolling registers and that will need maths to explain properly, using some pre-slanted texture as shown in the ripped contents of DKC2.

First immediate thought after I realised that it could be more than welcome in the pyramid level of Bilou's Dreamland was that it is actually an instance of the raycasting algorithm. Yeah, that infamous thing that turned ID software away from my beloved Commander Keen and sent them trashing the whole era of 2D platformers with first-person shooters. No wonder why, despite my affinty for maths and software optimization, I never ever felt tempted to code one myself. But hey, do it vertically instead of horizontally, and this is precisely what we need to decide whether to show floor, ceiling, wall or cut-through floor-to-ceiling structure.

So before trying to reconstruct the algorihtm that might have been used on SNES, let's see what it would cost us.

• the background scene must be structured along a 2D grid. I'd say 64x64 pixels would be fine by me
• For every scanline , we will have to step through the grid, one tile at a time, essentially checking whether one more "depth" step takes us farther than one "height" step in our case.
• We need a direction vector associated with every scanline. That implies 192 square roots per frame, but hopefully, those computations are the same for every frame: they depend on the camera-to-screen distance and define angle used to trace through each pixel. They could be pre-computed even at compile time and stored in a look-up table.

So for every scanline Ys of the screen, (DDA) raycasting will give us a pair of (Zw, Yw) coordinates in the world that is shown on that scanline. Most likely, we don't want to compute the distance to Zw, Yw nor use that distance to adjust scrolling speed. Instead, Zw should directly be used to decide the scrolling speed. Well, unless we're on a horizontal surface, that is. Well, I can't help thinking this is overgeneral and overkill, despite übercool.

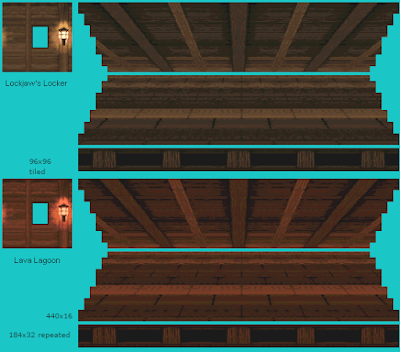
The trick in the SNES DKC2 implementation is that we have pre-rendered floors and ceilings. They already feature some depth-of-field effect. if you use them as-is. And being 440px wide, they're significantly larger than the screen (256 pixels iirc). Where does that 440 value come from ? Well, I guess this is screen_width + pattern_width, as the flat stripe shows a repeating pattern of 184 pixels. So whereever you are in the pattern, you can always have at least one full scanline ahead. The most distant line of the ceiling has only 96 pixels between two patterns, matching exactly the size of the tiled background wall. That means if the 'front' part is moving exactly at 1 pixel / frame, the tiled part should be moving at 0.52 pixel/frame so that Thales theorem is satisfied.

That size difference also tell us how far away the tiled parallax layer should be from the 184x32 parallax layer (and thus how deep the floor/ceiling objects are): they're as far from each other as the 184x32 layer is from the "camera"

  s16 xref = REG_BG1HOFS;
  s16 yref = (offset >> 2) % 192;
  s16 xamp = xref + xref / 2;
  s16 yamp = yref + yref / 2;
  int ytrigger = 224 - yamp;
  int btrigger = 192 - yref;
  int i, j;
  for (i = 0, j = 0; j < N; j++, i += 2) {
    if (j > ytrigger && j < ytrigger + 64 
        || j > ytrigger + 256) {
      data[i] = xamp;
      data[i+1] = yamp + 30;
    } else {
      data[i] = xref;
      data[i+1] = yref + (j >= btrigger ? 128 : 64);
    }
  }

That doesn't make the 3D-effect of DKC yet, but at least it gets me synchronous parallax with a single hardware layer.

Next step: find the zones where ceiling and floor should be shown. And there, trials and errors became too complicated to figure out. Hopefully, I found a way to analyze the problem with maths. Most of what's computed is derived from that "yref" value, which is normally the input from camera position. What I need to do is use that yref as horizontal axis and study how "triggers" that define top or bottom of areas evolve, cross and areas overlap appear or disappear. And once the (simple) maths were written, it took only half an hour to write the code to do it right.

With this graphics, that's the best I can do... let's see how it follows up once I have dedicated background.

Oh, and while I'm at it, there's a stunning online tool out there, to visit every map of every DKC SNES game: the DKC-atlas.